Estas son unas nociones generales sobre el dibujo técnico comparándolo con el artístico (extrapolando):
El dibujo artístico pretende provocar emociones.
El dibujo técnico pretende transmitir una información técnica con exactitud, encaminada normalmente a la fabricación de un objeto.
La obra artística va firmada por el autor para atribuirse su valor artístico.
El plano suele ir firmado por un técnico que se responsabiliza de él como documento en el que va a basarse la construcción de algo.
Las dimensiones de un lienzo pueden escogerse libremente.
Las dimensiones de un plano están normalizadas, y en el plano se traza un recuadro un casillero, y se centra el dibujo
El dibujo artístico no se ajusta a normas.
El dibujo técnico se ajusta estrictamente a una normalización.
Para el dibujo técnico se requiere conocer unas técnicas de manejo de instrumentos, escalas, acotaciones, simbología, etc.
El dibujo artístico suele realizarse en colores, y el técnico no
Te interesa conocer el dibujo técnico no solo para aprender a dibujar planos, sino además para poder interpretar toda la información que contiene los planos.
NORMALIZACION
La normalización del dibujo técnico es el conjunto de normas que regulan todos los elementos que intervienen en el diseño grafico.
Regulando: los tamaños de papel a utilizar (formatos), la dureza de las minas, la obtención de vistas, la escala adecuada en cada caso, la forma de acotar, la rotulación, los tipos de líneas, las simbología, la representación de elementos como roscas, engranajes, etc.
Las normas ISO. son las internacionales, Las normas UNE son las Españolas (Una Norma Española), Las DIM Alemanas. Las ASA Norteamericanas, las UNI Italianas, Las IRAM las Argentinas (Instituto de Racionalización Argentino de Medidas)
ESCALAS
Cuando queremos representar un objeto en una hoja de papel, debemos recurrir a las escalas que es un método gráfico que nos permite agrandar o achicar ese objeto de acuerdo al grado de detalle o minuciosidad que se requiera. Estas nos permiten hacer el dibujo guardando las proporciones del objeto real.
Las escalas pueden ser:
ü Real (medida que el objeto tiene en la realidad).
ü De ampliación
ü De reducción
La escala siempre debe ir debajo de cada dibujo, y las medidas indicadas deben ser las reales y no las que usamos para hacer el dibujo.
Reducción
Los pasos a seguir para la aplicación de una escala son los siguientes:
Por ejemplo si queremos representar un árbol que tiene las siguientes dimensiones: altura total 10 m ; altura de la copa al piso 4 m ; ancho de la copa 4m.
1) Para dibujar el árbol de estas dimensiones, tenemos que utilizar una escala de reducción para que el dibujo quepa en la hoja.
2) La elección de la escala a utilizar, saldrá de dividir las medidas en cm. cuantas veces queramos achicar el dibujo, por ej. dividimos por: 10, 20, 25, 100 casi siempre por números enteros.
3) Se procede al pasaje de todas las medidas a cm. que es la medida de longitud que vamos a usar en la hoja de nuestra carpeta.
Ejemplo: Pasamos a cm.
Dividimos por 100 todas las medidas del árbol
Por lo tanto la altura total del árbol, ancho de la copa, altura de la copa al piso se representarán con: 10 cm .; 4 cm .; 4 cm .
Tenemos que decir que tipo de escala hemos adoptado después de todo este procedimiento, y la escala usada es 1: 100
1 corresponde al metro, 100 es las veces que hemos dividido al metro.
En este ejemplo hemos dividido por 100, pero podemos dividir por cualquier número hasta encontrar la medida que nos sea más cómoda para el dibujo.
Ampliación
En el caso de ampliar el dibujo, haremos a la inversa, es decir, multiplicaremos las medidas del objeto, que se supone que es pequeño, causa por la cual se amplia, por la cantidad de veces que queremos agrandarlo.
Expresaremos la escala anteponiendo el número que corresponde a la cantidad de veces que multiplicamos al metro, por ej. 2: 1, 3: 1 y así sucesivamente.
Cuando nos dan un objeto para dibujar, y nos dicen que lo dibujemos en escala real, debemos repetir las medidas que el objeto tiene en la realidad.
Podemos definir que una escala: ES LA RELACIÓN QUE EXISTE ENTRE EL DIBUJO Y EL OBJETO A REPRESENTAR.
ACOTACION
Acotar es indicar las dimensiones que tiene el objeto que representamos
· Líneas auxiliares de cota
· Flecha
· Cifras y símbolos en algunas ocasiones
Las líneas de cota se disponen paralelamente a la dimensión que se quiere acotar, y lleva flecha en sus extremos.
Las líneas auxiliares de cota suelen ser perpendiculares a las de cotas.
Tanto las líneos de cota como las auxiliares se dibujan con líneas finas.
Para favorecer la claridad es aconsejable sacar las líneas de cotas fuera del dibujo.
Es importante que ni la línea de cota ni las líneas auxiliares formen intersección entre si ni con el dibujo. Para evitar que se crucen, las cotas mayores se dibujan más alejadas del objeto que las más pequeñas.
Nunca debe emplearse un eje como línea de cota.
LAS LÍNEAS
Cada tipo de linea tiene una expresividad propia y un significado diferente en el dibujo técnico.
- La línea gruesa se emplean para representar los contornos y aristas visibles de los cuerpos.
- La línea fina se emplea para las líneas de cata rallados. etc.
- La línea de trazos: se emplea para, las aristas ocultas de las piezas.
- La línea de trazo y punto se emplea para representar los ejes de simetría.
- La línea de trazo y dos puntos: se emplea para representar la indicación de por donde se da un corte
LAS VISTAS
Determinación de las vistas:
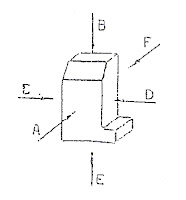
De acuerdo con el diedro fundamental y a los planos paralelos al mismo, se obtienen tres vistas fundamentales A. B y C y tres vistas principales D, E y F. las flechas indican el sentido perpendicular del observador con respecto a cada plano de proyección.
- Vista anterior: la que se obtiene al observa el cuerpo o pieza de frente, considerando esta posición como inicial del observador (A).
- Vista superior: la que se obtiene al observar el cuerpo o pieza desde arriba (B).
- Vista lateral derecha: la que se obtiene al observar el cuerpo o pieza de la izquierda de la posición inicial del observador (C).
- Vista lateral izquierda: la se obtiene al observar el cuerpo o pieza desde la derecha de la posición inicial del observador (D).
- Vista inferior: la que se obtiene al observar el cuerpo o pieza desde abajo (E).
- Vista posterior: la que se obtiene al observar el cuerpo o pieza desde atrás (F).
PROYECCIONES ORTOGONALES CONCERTADAS O MÉTODO MONGE
Introducción
“Desde los tiempos más antiguos, los arquitectos, carpinteros, etc. usaban procedimientos más o menos ingeniosos para representar los objetos que tenían que construir, pero estos procedimientos empíricos, por más ingeniosos que fueran, no respondían a reglas y principios fijos. Recién a fines del siglo XVIII (1780), el ilustre geómetra Monge ha reunido y formado un cuerpo de doctrina bajo el nombre de "Geometría Descriptiva”, en que no solamente expone bajo principios matemáticos la representación de los cuerpos, sino que también desenvuelve, abriendo nuevos horizontes, el estudio de las propiedades geométricas abstractas.”
Francisco Canale, 1886*1
El sistema de vistas, denominado proyección Monge
Permite ver las distintas caras del objeto, cada una vista de frente, como si nos colocáramos en distintos lugares para ver el objeto. Se representan en este tipo de sistema la vista frontal, la vista superior y la vista lateral izquierda. Observemos los dibujos para comprenderlo mejor:
Éstas son todas las vistas posibles de un objeto. Vemos que algunas de ellas no necesitan ser dibujadas para representar el objeto. La lateral izquierda es similar a la derecha y la información que veo en la posterior está indicada en la frontal.
Contiene los objetos pero éstos tienen deformidades más acusadas. Teniendo los ejes principales X, Y, Z
Perspectiva caballera y caballera reducida
Para hacer una perspectiva caballera podemos seguir dos procedimientos:
a) hacerla sobre papel normal utilizando los 45 de la escuadra para trazar la inclinación del eje OY.
Hacerla sobre papel cuadriculado (directamente o colocándolo debajo del papel vegetal).
Trazamos los ejes dibujamos la cara frontal con las medidas que tiene, después trazamos las líneas oblicuas y llevamos sobre ella las medidas de las aristas y terminamos el dibujo trazando paralelas.
Este proceso se simplifica algo cuando se hace sobre papel cuadriculado. (en este caso para trazar las líneas oblicuas utilizaremos las diagonales de la cuadricula).Para dibujar la perspectiva de cualquier figura imaginaremos inscripta en un paralelepípedo, sacaremos la perspectiva de este y después completaremos la figura.
En el caso de perspectivas caballera reducida debemos dibujarla con un coeficiente de reducción en el eje Y: K= ½ (esto quiere decir que en el eje Y a todas las distancias las tendremos que dividir por dos).
Es utilizada cuando una pieza, por su complejidad, no es fácil de interpretar a través de sus vistas como, por ejemplo, la de los manuales de instrucciones de todo tipo de maquinaria.
PERSPECTIVA ISOMÉTRICA
La perspectiva isométrica es una técnica de representación gráfica de un objeto tridimensional en dos dimensiones, donde los tres ejes coordenados ortogonales al proyectarse forman ángulos iguales de 120º cada uno sobre el plano. Las dimensiones de los cuerpos paralelas a los ejes se representan a una misma escala.
La perspectiva isométrica tiene la ventaja de permitir la representación a escala, pero sin reflejar la disminución aparente que produce la distancia entre el ojo humano y el objeto.
Los ejes de las X y de las Y se sitúan a 30º de la línea horizontal, pues son los que corresponden al plano horizontal. El eje Z se sitúa perpendicular la línea del horizonte, formando ángulos de 60º con los anteriores.
De este modo, veremos la cara superior de un cubo formando 120º sus aristas más próximas al observador.
El nombre de la perspectiva, isométrica, deriva del griego y significa igual medida. Esto debido a que la escala de medición es la misma a lo largo de cada eje, cosa que no sucede con las otras perspectivas.
Esta perspectiva tiene el inconveniente de no marca la profundidad de los objetos que muestra, debido a que las líneas que representan las dimensiones son paralelas y los objetos no empequeñecen con la distancia.
Aplicaciones de la perspectiva isométrica:
La perspectiva isométrica tiene sus aplicaciones en algunos ejemplos arquitectónicos, para representar algunas arquitecturas imposibles.
También resulta de utilidad en el diseño industrial pues representa las piezas desde diferentes puntos de vista, perpendicular a los ejes coordenados naturales.
En arquitectura permite visualizar los volúmenes independientemente del punto de vista del observador.